Perchè nascondere che cosa succede nei primi 14 giorni post inoculazione?

Sono stati pubblicati numerosi articoli che mostrano quanto i vaccini proteggano le persone dopo la seconda dose. Alcuni di questi effetti sono però un'illusione.

L'effetto si verifica a causa di misurazioni imprecise e di un fenomeno chiamato survival bias

Il survivorship bias o survival bias o pregiudizio di sopravvivenza è l'errore logico che si commette allorquando, per valutare una situazione, si prendano in considerazione solo gli elementi (persone o cose) che hanno superato un determinato processo di selezione, trascurando i restanti.

Sarebbe come valutare la qualità di una scuola di nuoto, che privilegia la tecnica dei nuotatori dopo averle gettate in mezzo all'oceano, lasciandole per un paio d'ore e rivendicando il merito di quanto bene sappiano nuotare i sopravvissuti. Dopo due ore infatti, le uniche persone rimaste sarebbero quelle che sapevano già nuotare e forse alcuni che di necessità virtù, hanno imparato a nuotare nel modo più difficile! Le povere anime che sono annegate nel frattempo, non fanno nemmeno il conto. Attribuire la capacità di nuoto delle persone restanti, all'allenatore che si è presentato 2 ore dopo, darebbe ovviamente un'immagine molto fuorviante. Così come sottolineare che nessuno è annegato nelle lezioni successive, sarebbe ugualmente fuorviante nel determinare il successo della scuola di nuoto per rimanere in esempio. 

Con la vaccinazione covid c'è un periodo di due settimane dopo la vaccinazione che non è incluso nei dati . La motivazione addotta è che i vaccini impiegano del tempo per indurre gli anticorpi e quindi i dati delle prime due settimane non sono rilevanti. Ovviamente questo è viziato. E se i vaccini avessero effetti deleteri immediatamente visibili, che non hanno nulla a che fare con la produzione di anticorpi?

Un esempio è l'alto tasso di fuoco di Sant'Antonio osservato dopo la vaccinazione contro il covid, suggerendo che c'è un problema con la riattivazione virale. Questo potrebbe spiegare perché i tassi di infezione da Sars-CoV-2 sono effettivamente più alti nei vaccinati rispetto ai non vaccinati nelle prime due settimane dopo la vaccinazione.

L'effetto dell'eliminazione delle prime due settimane è una distorsione dei dati. Se le persone vengono infettate e muoiono durante quel periodo, questo deve essere incluso. La possibilità che il vaccino stesso possa esercitare un effetto sul tasso di infezione, non può essere trascurata e l'intero set di dati deve essere incluso per valutare accuratamente l'efficacia. Solo misurando il periodo successivo al maggior rischio di infezione (0-14 giorni) è possibile essere ingannati dai risultati.

Oltre a non avere senso in termini di rischio individuale, rimuovere questo periodo di tempo, ha un ampio impatto sulla comunità. Se il vaccino in effetti provoca un picco di infezioni durante le prime due settimane, ciò aumenterà inevitabilmente la diffusione e porterà a un aumento del numero di infezioni in quella comunità durante quel periodo. Pertanto, la valutazione dell'impatto del programma di vaccinazione deve includere non solo l'effetto sull'individuo, ma l'impatto sulla comunità più ampia.

Questo punto è di particolare rilevanza nelle comunità dove gli individui vengono vaccinati contemporaneamente, come le scuole, case di cura e gli ospedali. In questo modo è come se venisse “accelerata” l'ondata di infezioni (e decessi). Ma a causa dell'esclusione dei decessi precedenti (1-14 giorni), siamo indotti a pensare che i vaccini fossero più efficaci di quanto non fossero in realtà.

---

---

Osservando solo il periodo successivo e vedendo meno morti durante quel periodo, si creò l'illusione che le vite fossero state salvate. Ciò è evidente nei dati di molti paesi dopo l’avvio della campagna vaccinale. Il grafico sotto, mostra il Regno Unito rispetto all'Europa, poiché il Regno Unito come sappiamo è stato uno dei primi (con Israele) e il più veloce ad avviare la campagna vaccinale nella popolazione.

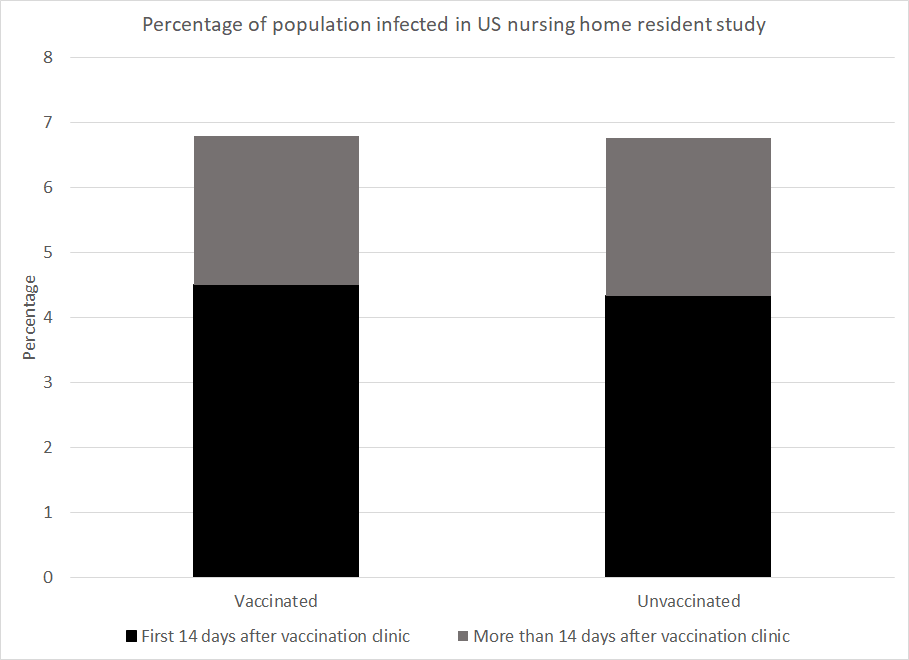
Esaminiamo ora alcuni esempi specifici, ad esempio questo studio sui residenti di case di cura negli Stati Uniti. I risultati mostrano che nel corso dello studio il 6,9% della popolazione vaccinata e il 6,7% della popolazione non vaccinata sono state infettate. Tuttavia, decidendo di escludere i primi 14 giorni dopo la vaccinazione, l'area grigia per il gruppo vaccinato viene confrontata con l'area nera e grigia combinata per i non vaccinati. Ciò potrebbe portare alla pretesa di un'efficacia del vaccino del 79% contro le infezioni. Gli autori di questo studio sono stati abbastanza onesti da condividere i dati grezzi senza affermare tale valutazione.

Tuttavia, numerosi studi si sono basati su questo trucco per affermare l'efficacia del vaccino. Gli esempi più evidenti di ciò sono lo studio sperimentale Pfizer originale e lo studio AstraZeneca .

Per fare un secondo esempio, un documento danese ha misurato i numeri di infezione negli operatori sanitari e nei residenti delle case di cura. Prima dell'inizio del programma di vaccinazione il 4,8% degli operatori sanitari era stato infettato e lo era il 3,8% dei residenti delle case di cura. Lo studio si è concluso alla fine dell'ondata invernale danese, dopo che il 95% dei residenti delle case di cura e il 28% degli operatori sanitari era stato vaccinato. Dato il tasso di vaccinazione più basso negli operatori sanitari, ci si potrebbe aspettare che nel complesso stessero peggio.. Invece la percentuale di contagiati alla fine dell'ondata era del 7,0% tra gli operatori sanitari e del 7,7% tra i residenti nelle case di cura.

Quanta dell'efficacia del vaccino, riportata nella ricerca sul covid, è davvero una misura del bias di sopravvivenza accoppiato con l'immunità acquisita naturalmente?

Questa è una domanda critica e riteniamo che nessuna pretesa di efficacia di questi farmaci dovrebbe essere fatta, senza aver prima affrontato questo problema.

---

---